Class 10 Maths Chapter 1 Exercise 1.2 Solution In Hindi Medium
दोस्तों पिछले पोस्ट में मैं आपको प्रश्नावली 1.1 का हल कर दिया है, इस पोस्ट में Class 10 Maths Chapter 1 Exercise 1.2 Solution In Hindi Medium में Solve किया गया हैं जो आपके तैयारी में चार चंद लगा देगा । दोस्तों इस website पर आपको पूरे Book का Solutions हिन्दी और English माध्यम में क्रमानुसार मिलता रहेगा आप अपनी तैयारी निरंतर जारी रखिए और साथ ही साथ Notes भी बनाते रहिए । इस Link पर Click करके आप Video Solutions भी देख सकते हैं।
प्रश्नावली 1.2 (पृष्ठ संख्या 13)
प्रश्न 1 निम्नलिखित संख्याओं को अभाज्य गुणनखंड के रूप में व्यक्त कीजिये:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
उत्तर-
(i) 
(ii)
(iii)
(iv)
(v)
प्रश्न 2 पूर्णांकों के निम्नलिखित युग्मों के LCM और HCF ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = LCM × HCF है:
(i) 26 और 91
(ii) 510 और 92
(iii) 336 और 54
उत्तर- (i) 26 = 2 × 13
91 = 7 × 13
सार्व गुणनखंड = 13
∴ HCF = 13
LCM = 2 × 7 × 13 = 182
अब, जाँच,
दो संख्याओं का गुणनफल = LCM × HCF
N1 × N2 = LCM × HCF
26 × 91 = 13 × 182
2366 = 2366
सिद्ध हुआ|
(ii) 510 = 2 × 3 × 5 × 17
92 = 2 × 2 × 23
सार्व गुणनखंड = 2
∴ HCF = 2
LCM = 2 × 2 × 3 × 5 × 17 × 23 = 23460
अब, जाँच,
दो संख्याओं का गुणनखंड = LCM × HCF
N1 × N2 = LCM × HCF
510 × 92 = 2 × 23460
46920 = 46920
सिद्ध हुआ|
(iii) 336 = 2 × 2 × 2 × 2 × 3 × 7
54 = 2 × 3 × 3 × 3
सार्व गुणनखंड = 2 × 3
∴ HCF = 6
LCM = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7 = 3024
जाँच,
दो संख्याओं का गुणनफल = LCM × HCF
N1 × N2 = LCM × HCF
336 × 54 = 6 × 3024
18144 = 18144
सिद्ध हुआ|
प्रश्न 3 अभाज्य गुणनखंड विधि द्वारा निम्नलिखित पूर्णांकों के LCM और HCF ज्ञात कीजिए:
(i) 12, 15 और 21
(ii) 17, 23 और 29
(iii) 8, 9 और 25
उत्तर- (i) 12 = 2 × 2 × 3
15 = 5 × 3
21 = 7 × 3
सार्व गुणनखंड = 3
HCF = 3
LCM = 3 × 2 × 2 × 5 × 7 = 420
(ii) 17 = 1 × 17
23 = 1 × 23
29 = 1 × 29
HCF = 1
LCM = 17 × 23 × 29 = 11339
(iii) 8 = 2 × 2 × 2
9 = 3 × 3
25 = 5 × 5
यहाँ 1 को छोड़कर अन्य कोई सार्व गुणनखंड नहीं है:
∴ HCF = 1
LCM = 2 × 2 × 2 × 3 × 3 × 5 × 5
= 8 × 9 × 25
= 1800
प्रश्न 4 HCF (306, 657) = 9, दिया है। LCM (306, 657) ज्ञात कीजिए।
उत्तर-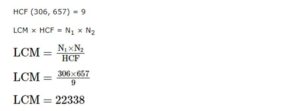
प्रश्न 5 जाँच कीजिए कि क्या किसी प्राकृत संख्या n के लिए संख्या 6n अंक 0 पर समाप्त हो सकती है।
उत्तर- 6n का अभाज्य गुणनखंड = (2 × 3)n
जबकि, कोई प्राकृत संख्या जो शून्य पर समाप्त होती है उसके अभाज्य गुणनखंड (2 × 5)n के रूप का होता है।
अत:, 6n शून्य पर समाप्त नहीं होगी।
प्रश्न 6 व्याख्या कीजिए 7 × 11 × 13 + 13 और 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 भाज्य संख्या क्यों है?
उत्तर- माना A = 7 × 11 × 13 + 13
= 13(7 × 11 + 1)
= 13(77 + 1)
= 13 × 78
अत: यह एक भाज्य संख्या है क्योंकि इसके अभाज्य गुणनखंड में 1 को छोड़कर अन्य दो गुणनखंड हैं।
इसी प्रकार,
माना B = 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
= 5(7 × 6 × 4 × 3 × 2 × 1 + 1)
= 5 × (1008 + 1)
= 5 × 1009
अत: यह भी एक भाज्य संख्या है क्योंकि इसके भी अभाज्य गुणनखंड में 1 को छोड़कर अन्य दो गुणनखंड हैं।
प्रश्न 7 किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है। इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं। मान लीजिए वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारंभ करके एक ही दिशा में चलते हैं। कितने समय बाद वे पुनः प्रांरभिक स्थान पर मिलेंगे?
उत्तर- एक चक्कर में सोनिया 18 मिनट लेती हैं।
रवि एक चक्कर में 12 लगाता है।
वे दोनों एक ही स्थान पर LCM(18, 12) मिनट के बाद मिलेंगे।
अत:
18 = 2 × 3 × 3
12 = 2 × 2 × 3
HCF = 2 × 3 = 6
= 36 मिनट

















