दोस्तों इस पोस्ट में आपको कक्षा -10 अध्याय -6 त्रिभुज के सभी महत्वपूर्ण सूत्र को बहुत ही आसान भाषा में समझाने का प्रयास किया है जो आपके पढाई में बहुत हेल्प करेगा ……
अध्याय-6: त्रिभुज
त्रिभुज क्या है
तीन रेखाखण्डों से घिरी हुई समतलीय आकृति त्रिभुज कहलाती है। त्रिभुज को ∆ से निरूपित किया जाता है। एक त्रिभुज की तीन भुजाएँ, तीन कोण और तीन शीर्ष होते हैं। त्रिभुज के तीनों कोणों का योग 180° होता है।
त्रिभुजों का वर्गीकरण
त्रिभुजों का वर्गीकरण निम्नलिखित दो आधार पर किया जा सकता है:
(i) भुजाओं के आधार पर
(ii) कोणों के आधार पर
भुजाओं के आधार पर त्रिभुज
भुजाओं के आधार पर त्रिभुज तीन प्रकार के होते हैं:
- विषमबाहु त्रिभुज
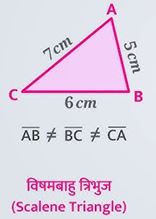
- समद्विबाहु त्रिभुज
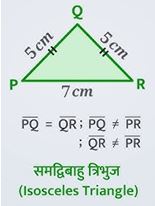
- समबाहु त्रिभुज
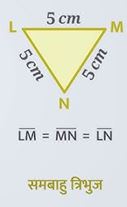
कोणों के आधार पर त्रिभुज
कोणों के आधार पर त्रिभुज तीन प्रकार के होते हैं:
- न्यून कोण त्रिभुज
- अधिक कोण त्रिभुज
- समकोण त्रिभुज
सभी सर्वांगसम आकृतियाँ समरूप होती हैं, परंतु सभी समरूप आकृतियों का सर्वांगसम होना आवश्यक नहीं है।
सर्वांगसम त्रिभुज
जब दो त्रिभुज की सारी भुजाओं एवं कोणों का माप समान होता है तो वे त्रिभुज सर्वांगसम होते हैं।
समरूप त्रिभुज
दो त्रिभुज समरूप होंगे यदि
(i) यदि दो त्रिभुजों में, संगत कोण समान हों, तो त्रिभुज समरूप होते हैं।
(ii) यदि दो त्रिभुजों की संगत भुजाएँ समानुपाती हों, तो त्रिभुज समरूप होते हैं।
(iii) यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा उन कोणों को बनाने वाली भुजाएँ समानुपाती हों, तो त्रिभुज समरूप होते हैं।
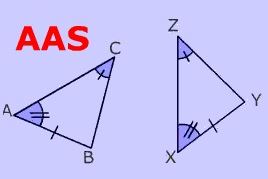
सर्वांगसमता के प्रकार
(i) AAS (कोण–कोण–भुजा):
यदि दो त्रिभुजों के कोणों के दो युग्म माप में बराबर हों, और संगत गैर–शामिल भुजाओं का एक युग्म लंबाई में बराबर हो, तो त्रिभुज सर्वांगसम होते हैं।
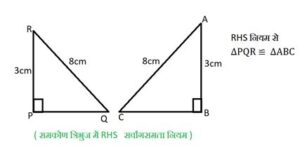
(ii) RHS (समकोण–कर्ण–पक्ष):
यदि दो समकोण त्रिभुजों के कर्णों की लंबाई समान है, और छोटी भुजाओं का एक युग्म लंबाई में समान है, तो त्रिभुज सर्वांगसम होते हैं।
कोणों के आधार पर त्रिभुज के प्रकार
कोणों के आधार पर त्रिभुज तीन प्रकार के होते हैं:
- न्यून कोण त्रिभुज: (उस त्रिभुज को कहते हैं जिसके तीनों कोण, न्यूनकोण (90° से कम) हों।)
- अधिक कोण त्रिभुज: (उस त्रिभुज को कहते हैं जिसका कोई एक कोण, अधिककोण (90° से अधिक) हो।)
- समकोण त्रिभुज: (जिसका एक कोण 90 अंश का (अर्थात, समकोण) हो।)
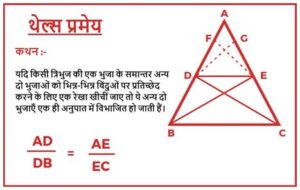
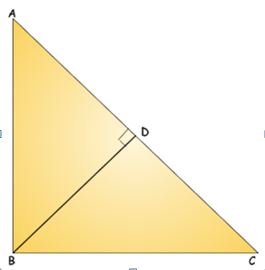
थेल्स (Thales) के प्रमेय
ज्यामिति में थेल्स के प्रमेय (Thales’ theorem) के अनुसार किसी भी वृत्त के परिधि पर स्थित तीन बिन्दुओं A, B तथा C हो तो कोण ABC का मान ९० अंश होगा यदि AC उस वृत्त का कोई व्यास हो। यह प्रमेय ‘अन्तःनिर्मित कोण प्रमेय‘ (inscribed angle theorem) का एक विशेष रूप है।